Oscillatory System with a 2:1 internal resonance

Consider the following system with 2 dofs

$\ddot{x}_1+c_1\dot{x}_1+x_1+b_1x_1x_2=\epsilon f_1\cos\Omega t$

$\ddot{x}_2+c_2\dot{x}_2+4x_2+b_2x_1^2=\epsilon f_2\cos\Omega t$

It follows that the system has 1:2 internal resonance. Given damping coefficients $c_{1,2}$ , nonlinear spring coefficients $b_{1,2}$ and forcing coefficients $f_{1,2}$ , the solution manifold of such system is of two dimension and can be parameterized by $(\epsilon,\Omega)$ in general. We use this example to demonstrate

SSM_isol2ep: continuation of equilibrium points in slow dynamics (corresponding to periodic orbits in regular time dynamics) in either forcing frequency $\Omega$ or forcing amplitude $\epsilon$ . The continuation here starts from an initial solution (isol);
SSM_ep2HB: continuation of Hopf bifurcation (HB) equilibrium points in slow dynamics (corresponding to Neimark-Sacker or torus (TR) bifurcation periodic orbits in regular time dynamics) in $(\Omega,\epsilon)$ . The continuation here starts from a saved ep solution, which is also a HB equilibrium point;
SSM_ep2SN: continuation of saddle-node (SN) bifurcation equilibrium points in slow dynamics (corresponding to SN bifurcation periodic orbits in regular time dynamics) in $(\Omega,\epsilon)$ . The continuation here starts from a saved ep solution, which is also a SN equilibrium point;
SSM_HB2po: continuation of periodic orbits in slow dynamics (corresponding to tori in regular time dynamics) in either forcing frequency $\Omega$ or forcing amplitude $\epsilon$ . The continuation here starts from a saved solution, which is a HB equilibrium point;
SSM_po2po: continuation of periodic orbits in slow dynamics (corresponding to tori in regular time dynamics) in either forcing frequency $\Omega$ or forcing amplitude $\epsilon$ . The continuation here starts from a saved periodic orbit solution;
SSM_po2SN: continuation of saddle-node periodic orbits in slow dynamics (corresponding to SN tori in regular time dynamics) in $(\Omega,\epsilon)$ . The continuation here starts from a saved po solution, which is also a SN periodic orbit;
SSM_po2SN: continuation of saddle-node (SN) periorid orbits in slow dynamics in $(\Omega,\epsilon)$ . The continuation here starts from a saved po solution, which is also a SN periodic orbit;
SSM_po2PD: continuation of periodic-doubling (PD) periorid orbits in slow dynamics (corresponding to PD tori in regular time dynamics?) in $(\Omega,\epsilon)$ . The continuation here starts from a saved po solution, which is also a PD periodic orbit;

clear all

Setup model

m = 1;
c1 = 5e-3;
c2 = 1e-2;
b1 = 1;
b2 = 1;
f1 = 1;
f2 = 0;
[mass,damp,stiff,fnl,fext] = build_model(c1,c2,b1,b2,f1,f2);


order = 2;
DS = DynamicalSystem(order);
set(DS,'M',mass,'C',damp,'K',stiff,'fnl',fnl);
set(DS.Options,'Emax',5,'Nmax',10,'notation','multiindex')

Forcing

epsilon = 1e-2;
kappas = [-1; 1];
coeffs = [fext fext]/2;
DS.add_forcing(coeffs, kappas, epsilon);

Linear Modal analysis

[V,D,W] = DS.linear_spectral_analysis();

 The first 4 nonzero eigenvalues are given as 
  -0.0025 + 1.0000i
  -0.0025 - 1.0000i
  -0.0050 + 2.0000i
  -0.0050 - 2.0000i

SSM computation

S = SSM(DS);
set(S.Options, 'reltol', 1,'notation','multiindex');
resonant_modes = [1 2 3 4]; % choose master spectral subspace
mFreq  = [1 2];              % internal resonance relation vector
order  = 3;                  % SSM expansion order
outdof = [1 2];             % outdof for output

SSM_isol2ep:

continuation of equilibrium points from an initial solution*

set(S.FRCOptions, 'initialSolver', 'fsolve');     % initial solution scheme
set(S.FRCOptions, 'coordinates', 'cartesian');    % coordinate representation
set(S.contOptions, 'PtMX', 200);                  % continuation setting
freqRange = [0.7 1.1]*imag(D(1));
FRC1 = S.SSM_isol2ep('isol_freq_tr_cart',resonant_modes,order,mFreq,'freq',freqRange,outdof);

sigma_out = 0
(near) inner resonance detected for the following combination of master eigenvalues
     0     1     1     0
     1     0     0     1
     2     0     0     0
     0     2     0     0

These are in resonance with the follwing eigenvalues of the master subspace
  -0.0025 + 1.0000i
  -0.0025 - 1.0000i
  -0.0050 + 2.0000i
  -0.0050 - 2.0000i

sigma_in = 2
Starting parallel pool (parpool) using the 'Processes' profile ...
Connected to parallel pool with 8 workers.
Manifold computation time at order 2 = 00:00:22
Estimated memory usage at order  2 = 1.24E-02 MB
Manifold computation time at order 3 = 00:00:00
Estimated memory usage at order  3 = 2.04E-02 MB

Equation solved.

fsolve completed because the vector of function values is near zero
as measured by the value of the function tolerance, and
the problem appears regular as measured by the gradient.


 Run='isol_freq_tr_cart.ep': Continue equilibria along primary branch.

    STEP   DAMPING               NORMS              COMPUTATION TIMES
  IT SIT     GAMMA     ||d||     ||f||     ||U||   F(x)  DF(x)  SOLVE
   0                          2.22e-14  1.47e+00    0.0    0.0    0.0

 STEP      TIME        ||U||  LABEL  TYPE            om         Rez1         Rez2         Imz1         Imz2          eps
    0  00:00:00   1.4716e+00      1  EP      1.0000e+00  -4.6331e-02   2.4582e-01  -4.5057e-02  -1.3493e-01   1.0000e-02
   10  00:00:00   1.4593e+00      2          9.9745e-01  -7.3152e-02   1.0509e-01  -3.7283e-03  -2.3117e-01   1.0000e-02
   20  00:00:00   1.4408e+00      3          9.9151e-01  -9.7552e-02   1.5971e-02   3.7959e-02  -2.0883e-01   1.0000e-02
   24  00:00:01   1.4363e+00      4  HB      9.8785e-01  -1.1063e-01   8.9007e-03   5.0638e-02  -2.0169e-01   1.0000e-02
   30  00:00:01   1.4323e+00      5          9.7641e-01  -1.5292e-01   1.6453e-02   7.5912e-02  -2.0716e-01   1.0000e-02
   40  00:00:01   1.4965e+00      6          9.1986e-01  -3.8637e-01   1.8126e-01   1.0059e-01  -2.8515e-01   1.0000e-02
   50  00:00:01   1.6749e+00      7          8.4211e-01  -6.7137e-01   4.6287e-01  -4.8162e-02  -1.6188e-01   1.0000e-02
   60  00:00:01   1.8543e+00      8          7.7252e-01  -8.0808e-01   5.5098e-01  -3.5383e-01   2.0155e-01   1.0000e-02
   70  00:00:01   1.9345e+00      9          7.4062e-01  -7.0325e-01   3.1295e-01  -6.6545e-01   5.3588e-01   1.0000e-02
   72  00:00:01   1.9349e+00     10  SN      7.4027e-01  -6.7737e-01   2.7047e-01  -6.9271e-01   5.5857e-01   1.0000e-02
   72  00:00:01   1.9349e+00     11  FP      7.4027e-01  -6.7737e-01   2.7047e-01  -6.9272e-01   5.5857e-01   1.0000e-02
   80  00:00:01   1.8758e+00     12          7.6103e-01  -4.0888e-01  -9.7064e-02  -8.1252e-01   5.8597e-01   1.0000e-02
   90  00:00:01   1.7032e+00     13          8.2316e-01  -8.4581e-02  -3.8031e-01  -7.1618e-01   3.2890e-01   1.0000e-02
  100  00:00:01   1.5061e+00     14          8.9639e-01   1.0381e-01  -3.4580e-01  -4.4736e-01   1.1064e-02   1.0000e-02
  110  00:00:01   1.3924e+00     15          9.4861e-01   1.1191e-01  -1.2710e-01  -1.8388e-01  -8.3432e-02   1.0000e-02
  115  00:00:01   1.3693e+00     16  FP      9.5793e-01   7.8288e-02  -4.3188e-02  -9.8575e-02  -4.6216e-02   1.0000e-02
  115  00:00:01   1.3693e+00     17  SN      9.5793e-01   7.8266e-02  -4.3152e-02  -9.8535e-02  -4.6188e-02   1.0000e-02
  120  00:00:01   1.3413e+00     18          9.4574e-01   4.6585e-02  -8.6126e-03  -5.1675e-02  -1.2239e-02   1.0000e-02
  130  00:00:02   1.2438e+00     19          8.7895e-01   2.0275e-02  -5.9680e-04  -2.1134e-02  -1.0285e-03   1.0000e-02
  135  00:00:02   9.9014e-01     20  EP      7.0000e-01   8.2644e-03  -3.6484e-05  -8.4032e-03  -6.8622e-05   1.0000e-02

 STEP      TIME        ||U||  LABEL  TYPE            om         Rez1         Rez2         Imz1         Imz2          eps
    0  00:00:02   1.4716e+00     21  EP      1.0000e+00  -4.6331e-02   2.4582e-01  -4.5057e-02  -1.3493e-01   1.0000e-02
   10  00:00:02   1.4683e+00     22          1.0026e+00  -5.6325e-03   2.5635e-01  -7.4481e-02   3.8663e-02   1.0000e-02
   20  00:00:02   1.4696e+00     23          1.0089e+00   3.7491e-02   1.9592e-01  -1.0480e-01   1.0559e-01   1.0000e-02
   21  00:00:02   1.4709e+00     24  HB      1.0096e+00   4.0124e-02   1.9450e-01  -1.0786e-01   1.0639e-01   1.0000e-02
   30  00:00:02   1.5082e+00     25          1.0220e+00   6.7963e-02   2.2411e-01  -1.6734e-01   1.0012e-01   1.0000e-02
   40  00:00:02   1.6353e+00     26          1.0447e+00   5.4554e-02   3.7757e-01  -3.1532e-01  -2.4978e-02   1.0000e-02
   50  00:00:02   1.7783e+00     27          1.0604e+00  -5.1924e-02   4.0756e-01  -4.3239e-01  -3.1776e-01   1.0000e-02
   60  00:00:02   1.8910e+00     28          1.0698e+00  -2.1801e-01   1.6061e-01  -4.6389e-01  -5.9581e-01   1.0000e-02
   70  00:00:02   1.9391e+00     29          1.0739e+00  -3.8153e-01  -2.6377e-01  -3.8812e-01  -6.0079e-01   1.0000e-02
   74  00:00:02   1.9372e+00     30  SN      1.0741e+00  -4.2246e-01  -3.8944e-01  -3.4267e-01  -5.2441e-01   1.0000e-02
   74  00:00:02   1.9372e+00     31  FP      1.0741e+00  -4.2246e-01  -3.8945e-01  -3.4266e-01  -5.2440e-01   1.0000e-02
   80  00:00:02   1.9059e+00     32          1.0730e+00  -4.7399e-01  -5.5431e-01  -2.2964e-01  -2.8291e-01   1.0000e-02
   90  00:00:02   1.8020e+00     33          1.0673e+00  -4.5854e-01  -5.1098e-01  -5.3717e-02   1.0048e-01   1.0000e-02
  100  00:00:02   1.6645e+00     34          1.0571e+00  -3.5199e-01  -2.5723e-01   6.9396e-02   2.7015e-01   1.0000e-02
  110  00:00:03   1.5412e+00     35          1.0441e+00  -2.0847e-01  -4.4822e-02   1.0646e-01   2.0147e-01   1.0000e-02
  118  00:00:03   1.4863e+00     36  SN      1.0380e+00  -1.1200e-01   9.9684e-03   8.4132e-02   8.5637e-02   1.0000e-02
  118  00:00:03   1.4863e+00     37  FP      1.0380e+00  -1.1200e-01   9.9692e-03   8.4130e-02   8.5630e-02   1.0000e-02
  120  00:00:03   1.4806e+00     38          1.0415e+00  -7.5420e-02   9.3264e-03   6.3921e-02   3.8295e-02   1.0000e-02
  130  00:00:03   1.5334e+00     39          1.0834e+00  -3.1001e-02   1.3279e-03   2.9174e-02   3.3935e-03   1.0000e-02
  133  00:00:03   1.5565e+00     40  EP      1.1000e+00  -2.5665e-02   7.9694e-04   2.4406e-02   1.9478e-03   1.0000e-02

FRCs on parametrisation space:

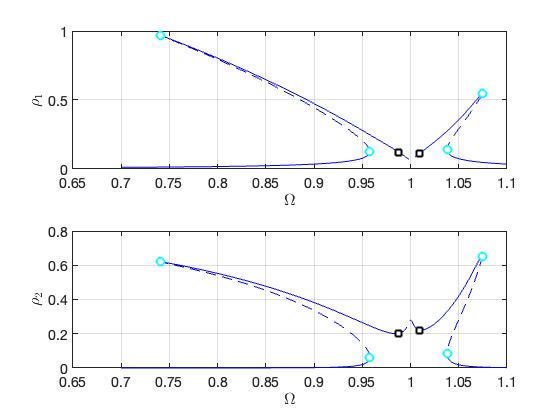
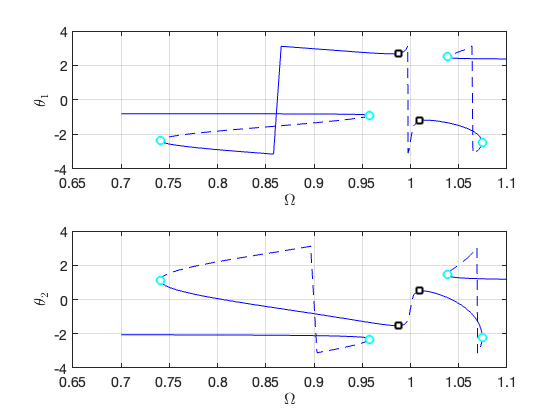
FRCs on physical space:

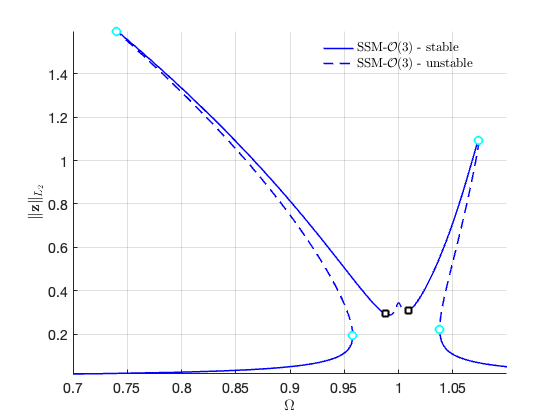
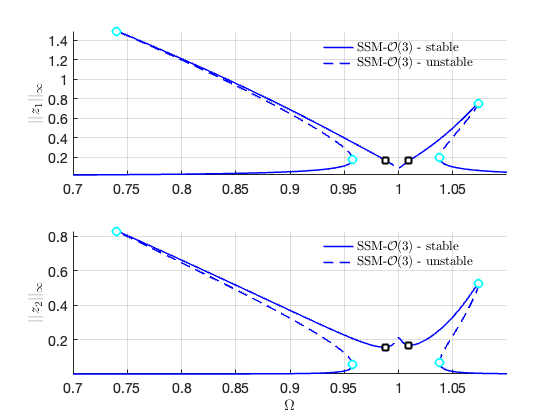
SSM_ep2HB:

continuation of Hopf bifurcation equilibrium points

set(S.contOptions, 'h_min', 1e-3);                   % coordinate representation
epsRange = [0.01 5]*epsilon;
HBlab = 4; % or you use HBlabs = coco_bd_labs(bd, 'HB') to find it
FRC2 = S.SSM_ep2HB('HB_tr_cart','isol_freq_tr_cart',HBlab,{freqRange,epsRange},outdof);

 Run='HB_tr_cart.ep': Continue Hopf equilibria from label 4 of run isol_freq_tr_cart.

    STEP   DAMPING               NORMS              COMPUTATION TIMES
  IT SIT     GAMMA     ||d||     ||f||     ||U||   F(x)  DF(x)  SOLVE
   0                          4.73e-10  1.75e+00    0.0    0.0    0.0

 STEP      TIME        ||U||  LABEL  TYPE            om          eps         Rez1         Rez2         Imz1         Imz2
    0  00:00:00   1.7502e+00      1  EP      9.8785e-01   1.0000e-02  -1.1063e-01   8.9007e-03   5.0638e-02  -2.0169e-01
    9  00:00:00   1.8472e+00      2  EP      9.6773e-01   5.0000e-02  -2.2843e-01  -1.0969e-01   1.7130e-01  -4.1531e-01

 STEP      TIME        ||U||  LABEL  TYPE            om          eps         Rez1         Rez2         Imz1         Imz2
    0  00:00:00   1.7502e+00      3  EP      9.8785e-01   1.0000e-02  -1.1063e-01   8.9007e-03   5.0638e-02  -2.0169e-01
   10  00:00:00   1.7322e+00      4          9.9653e-01   1.6005e-03  -4.2681e-02   5.0450e-02  -6.0246e-03  -5.2990e-02
   20  00:00:00   1.7327e+00      5          9.9943e-01   7.1494e-04  -1.9782e-02   3.6466e-02  -1.5449e-02  -1.9314e-02
   30  00:00:00   1.7337e+00      6          1.0003e+00   7.0551e-04  -1.6565e-02   3.6216e-02  -1.8425e-02  -1.8986e-02
   40  00:00:01   1.7347e+00      7          1.0009e+00   7.8230e-04  -1.5173e-02   3.9680e-02  -2.1812e-02  -1.9937e-02
   50  00:00:01   1.7441e+00      8          1.0043e+00   2.3995e-03  -1.8535e-03   9.6919e-02  -5.3519e-02  -5.2324e-04
   60  00:00:01   1.7994e+00      9          1.0116e+00   1.4772e-02   5.7628e-02   2.2774e-01  -1.2764e-01   1.5409e-01
   67  00:00:01   1.9482e+00     10  EP      1.0194e+00   5.0000e-02   1.3637e-01   3.7684e-01  -2.1366e-01   3.8628e-01

Bifurcations occur for the following forcing parameters:

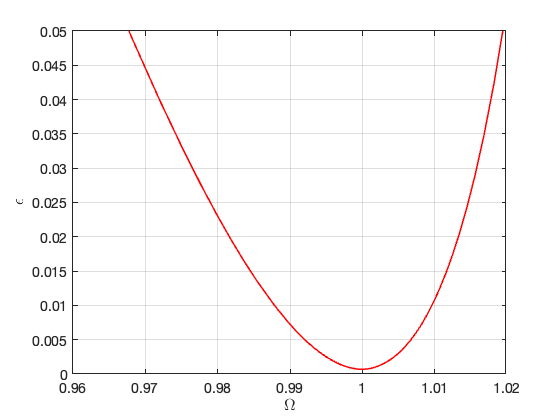
Bifurcations in parametrisation space:

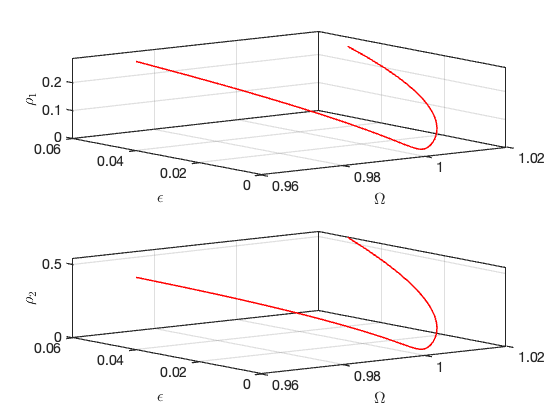
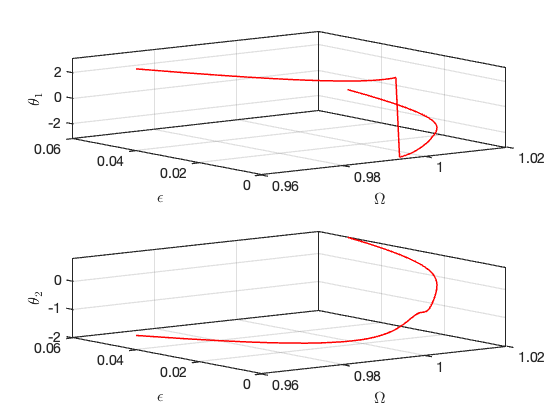
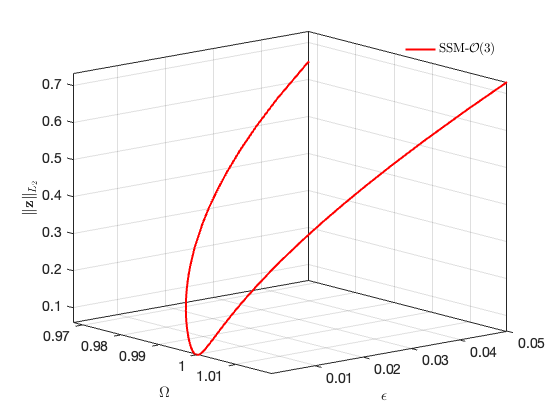
Bifurcations in physical space:

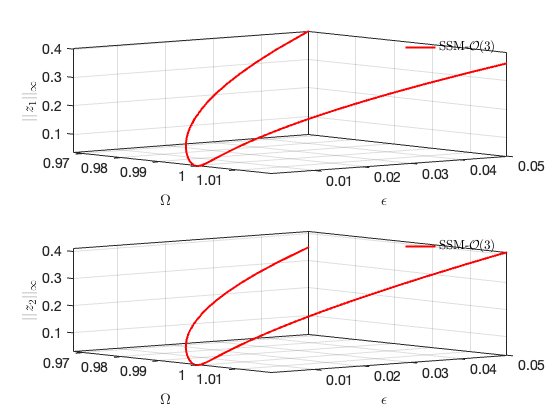
SSM_ep2SN:

continuation of saddle-node bifurcation equilibrium points

SNlab = 30;
FRC3  = S.SSM_ep2SN('SN_tr_cart','isol_freq_tr_cart',SNlab,{freqRange,epsRange},outdof);

 Run='SN_tr_cart.ep': Continue saddle-node equilibria from label 30 of run isol_freq_tr_cart.

    STEP   DAMPING               NORMS              COMPUTATION TIMES
  IT SIT     GAMMA     ||d||     ||f||     ||U||   F(x)  DF(x)  SOLVE
   0                          1.43e-08  2.18e+00    0.0    0.0    0.0

 STEP      TIME        ||U||  LABEL  TYPE            om          eps         Rez1         Rez2         Imz1         Imz2
    0  00:00:00   2.1801e+00      1  EP      1.0741e+00   1.0000e-02  -4.2246e-01  -3.8944e-01  -3.4267e-01  -5.2441e-01
   10  00:00:00   1.7795e+00      2          1.0231e+00   2.0562e-03  -1.1706e-01  -1.0021e-01  -7.0306e-02  -8.8809e-02
   20  00:00:00   1.7495e+00      3          1.0118e+00   9.2270e-04  -5.9827e-02  -5.1483e-02  -1.7282e-02  -1.6364e-02
   30  00:00:00   1.7448e+00      4  FP      1.0096e+00   7.0614e-04  -4.3675e-02  -3.1475e-02   2.9996e-04   7.1269e-03
   30  00:00:00   1.7448e+00      5          1.0096e+00   7.0743e-04  -4.3137e-02  -3.0346e-02   1.2777e-03   8.3480e-03
   40  00:00:00   1.7472e+00      6          1.0117e+00   9.8313e-04  -4.3556e-02  -1.9456e-02   1.3044e-02   2.1496e-02
   50  00:00:00   1.7602e+00      7          1.0206e+00   2.8826e-03  -6.4212e-02  -7.6223e-03   3.7424e-02   4.3857e-02
   60  00:00:00   1.8175e+00      8          1.0495e+00   1.7498e-02  -1.4724e-01   2.2904e-02   1.1779e-01   1.1777e-01
   68  00:00:00   1.9184e+00      9  EP      1.0792e+00   5.0000e-02  -2.5691e-01   6.7255e-02   2.2103e-01   2.3164e-01

 STEP      TIME        ||U||  LABEL  TYPE            om          eps         Rez1         Rez2         Imz1         Imz2
    0  00:00:00   2.1801e+00     10  EP      1.0741e+00   1.0000e-02  -4.2246e-01  -3.8944e-01  -3.4267e-01  -5.2441e-01
    4  00:00:00   2.8016e+00     11  EP      1.1000e+00   1.9116e-02  -6.7732e-01  -7.3953e-01  -5.4341e-01  -9.5562e-01

Bifurcations occur for the following forcing parameters:

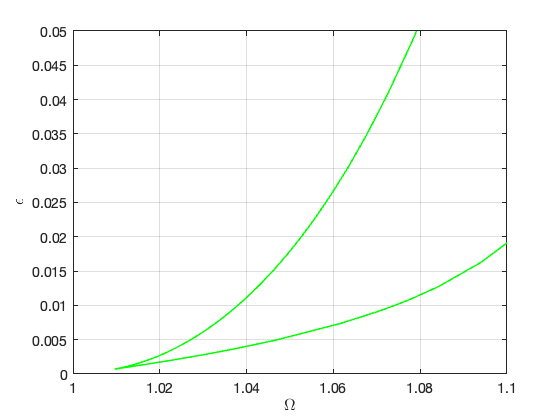
Bifurcations in parametrisation space:

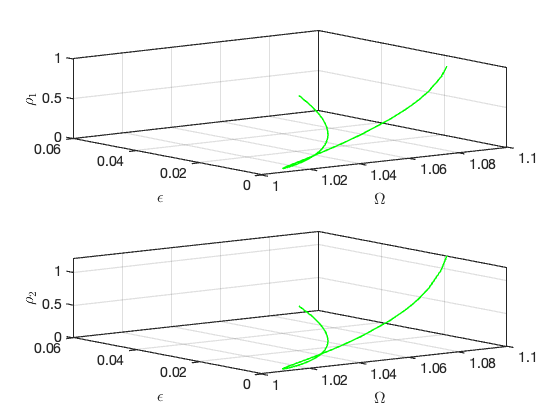
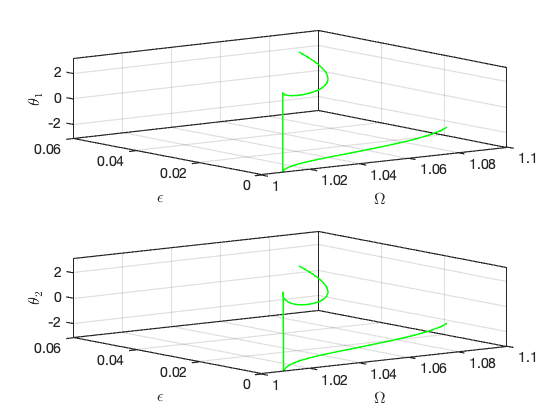
Bifurcations in physical space:

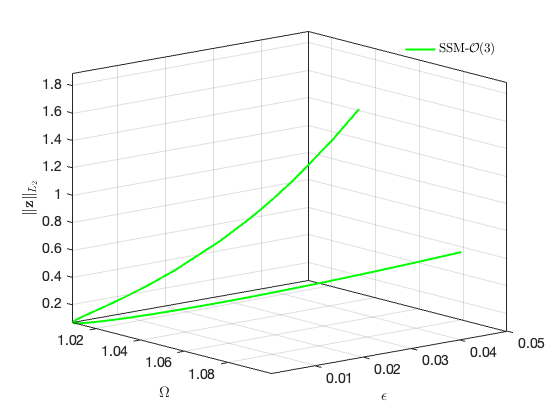
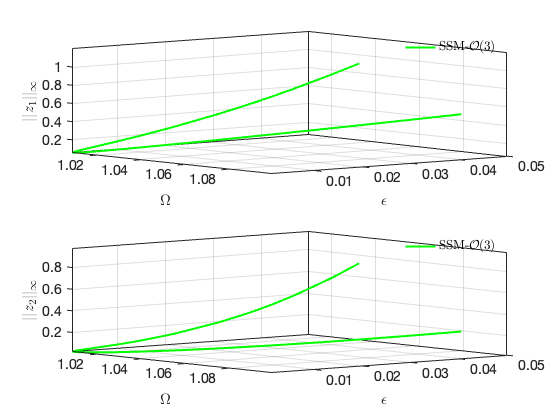
SSM_HB2po:

continuation of periodic orbits from HB equilibrium point

set(S.contOptions, 'NAdapt', 2, 'PtMX', 1500, 'h_max', 5, 'bi_direct', false);
set(S.FRCOptions, 'sampStyle', 'uniform');
set(S.FRCOptions, 'nPar', 51);
S.SSM_HB2po('HBpo1_tr_cart','isol_freq_tr_cart',HBlab,'freq',[0.97 1.02],outdof,'saveICs');

 Run='HBpo1_tr_cart.po': Continue periodic orbits born from a HB point with label 4 of run isol_freq_tr_cart.

    STEP   DAMPING               NORMS              COMPUTATION TIMES
  IT SIT     GAMMA     ||d||     ||f||     ||U||   F(x)  DF(x)  SOLVE
   0                          6.79e-06  2.74e+02    0.0    0.0    0.0
   1   1  1.00e+00  1.60e-03  8.74e-08  2.74e+02    0.0    0.0    0.0
   2   1  1.00e+00  2.67e-05  2.44e-11  2.74e+02    0.0    0.0    0.0
   3   1  1.00e+00  7.93e-08  8.16e-15  2.74e+02    0.0    0.0    0.0

 STEP      TIME        ||U||  LABEL  TYPE            om    po.period          eps
    0  00:00:00   2.7394e+02      1  EP      9.8785e-01   1.9370e+02   1.0000e-02
   10  00:00:00   2.7399e+02      2          9.8786e-01   1.9374e+02   1.0000e-02
   18  00:00:01   2.7878e+02      3  UZ      9.8800e-01   1.9712e+02   1.0000e-02
   20  00:00:01   2.9015e+02      4          9.8831e-01   2.0516e+02   1.0000e-02
   27  00:00:01   3.2124e+02      5  SN      9.8877e-01   2.2715e+02   1.0000e-02
   30  00:00:01   3.3640e+02      6          9.8824e-01   2.3787e+02   1.0000e-02
   36  00:00:02   3.3696e+02      7  UZ      9.8800e-01   2.3826e+02   1.0000e-02
..
 1500  00:01:24   4.4235e+02    291  EP      1.0098e+00  -3.1279e+02   1.0000e-02

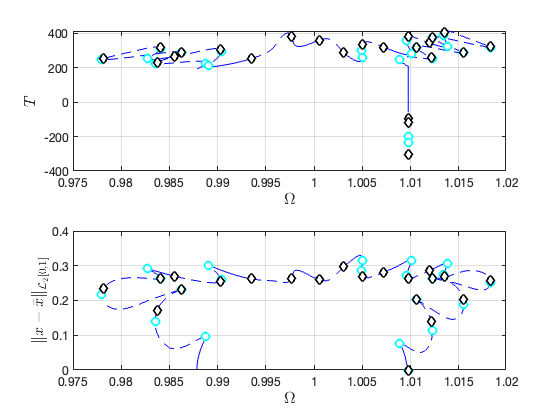
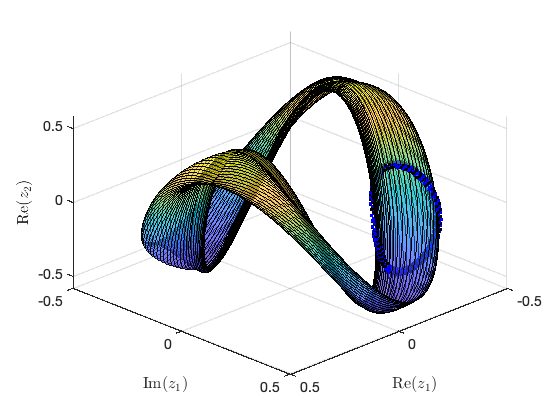
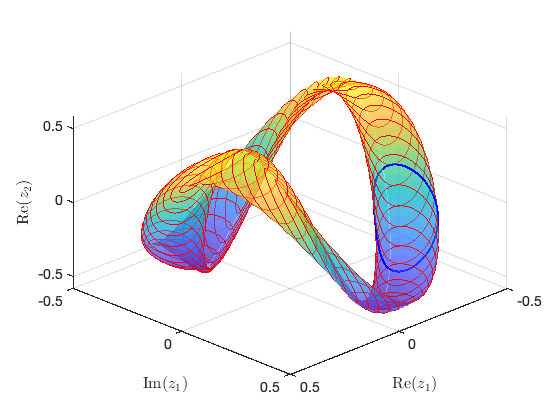
Constructing torus in reduced dynamical system

Illustration of the construction of torus in reduced dynamical system
Visualization of torus at (omega,epsilon)=(1.004000e+00,1.000000e-02)

 FRCs from ='HBpo1_tr_cart.po': generating torus in physical domain.

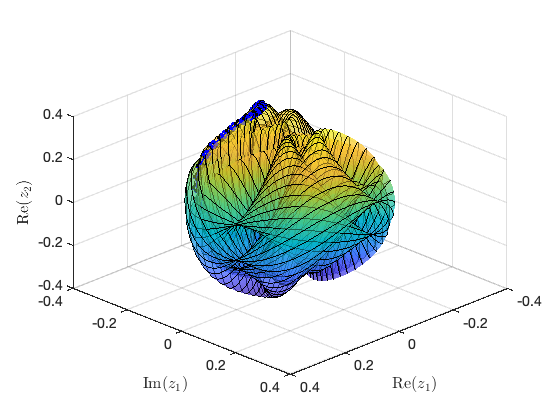
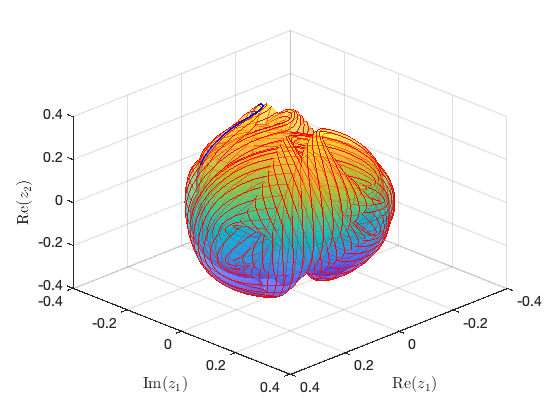
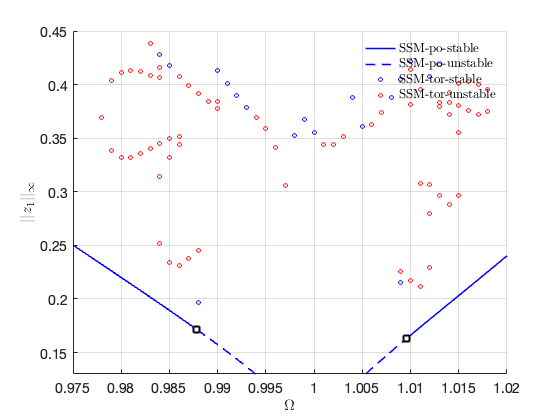
Plot quasiperiodic FRC

FRC of quasi-periodic orbits in physical coordinates

bd   = coco_bd_read('HBpo1_tr_cart.po');
labs = coco_bd_labs(bd, 'UZ');
nlab = numel(labs);
om = zeros(nlab,1);
Tp  = zeros(nlab,1);
x1amp = zeros(nlab,1); % amplitude of x1(t)
st = false(nlab,1);
x0 = cell(nlab,1);     % cross section of torus at t=0
for i=1:nlab
    sol = SSM_po_read_solution('HBpo1_tr_cart',labs(i));
    om(i) = sol.om;
    Tp(i) = sol.Tpo;
    x1i   = sol.xTr(:,1,:);
    x1amp(i) = norm(x1i(:),'inf');
    st(i) = sol.st;
    xx = permute(sol.xTr, [2,3,1]);
    x0{i} = xx(:,:,1);
end

ST = cell(2,1);
ST{1} = {'b--','LineWidth',1.5}; % unstable
ST{2} = {'b-','LineWidth',1.5};  % stable
legs = 'SSM-$\mathcal{O}(3)$-unstable';
legu = 'SSM-$\mathcal{O}(3)$-stable';
thm = struct();
thm.SN = {'LineStyle', 'none', 'LineWidth', 2, ...
  'Color', 'cyan', 'Marker', 'o', 'MarkerSize', 8, 'MarkerEdgeColor', ...
  'cyan', 'MarkerFaceColor', 'white'};
thm.HB = {'LineStyle', 'none', 'LineWidth', 2, ...
  'Color', 'black', 'Marker', 's', 'MarkerSize', 8, 'MarkerEdgeColor', ...
  'black', 'MarkerFaceColor', 'white'};

figure; hold on
plot_stab_lines(FRC1.om,FRC1.Aout_frc(:,1),FRC1.st,ST,legs,legu);
SNidx = FRC1.SNidx;
HBidx = FRC1.HBidx;
SNfig = plot(FRC1.om(SNidx),FRC1.Aout_frc(SNidx,1),thm.SN{:});
set(get(get(SNfig,'Annotation'),'LegendInformation'),...
'IconDisplayStyle','off');
HBfig = plot(FRC1.om(HBidx),FRC1.Aout_frc(HBidx,1),thm.HB{:});
set(get(get(HBfig,'Annotation'),'LegendInformation'),...
'IconDisplayStyle','off');
plot(om(st),x1amp(st),'bo','LineWidth',1,'MarkerSize',4); hold on
plot(om(~st),x1amp(~st),'ro','LineWidth',1,'MarkerSize',4); hold on
leg = legend('SSM-po-stable','SSM-po-unstable',...
    'SSM-tor-stable','SSM-tor-unstable','Interpreter','latex');
legend boxoff
xlabel('$\Omega$','Interpreter','latex');
ylabel('$||z_1||_{\infty}$','Interpreter','latex');
set(gca,'FontSize',14);
grid on, axis tight; legend boxoff;

axis([0.975,1.02,0.13,0.45])

SSM_po2po:

continuation of periodic orbits from saved solution

set(S.contOptions, 'NAdapt', 2, 'PtMX', 100, 'h_max', 5, 'bi_direct', true);
set(S.FRCOptions, 'sampStyle', 'cocoBD');
LAB = 3;
S.SSM_po2po('po2','HBpo1_tr_cart',LAB, 'amp', epsRange, outdof, 'saveICs');

 Run='po2.po': Continue periodic orbits born from saved solution with label 3 of run HBpo1_tr_cart.

    STEP   DAMPING               NORMS              COMPUTATION TIMES
  IT SIT     GAMMA     ||d||     ||f||     ||U||   F(x)  DF(x)  SOLVE
   0                          2.96e-15  2.79e+02    0.0    0.0    0.0

 STEP      TIME        ||U||  LABEL  TYPE           eps    po.period           om
    0  00:00:00   2.7877e+02      1  EP      1.0000e-02   1.9712e+02   9.8800e-01
    5  00:00:00   2.7729e+02      2  FP      9.8490e-03   1.9607e+02   9.8800e-01
    5  00:00:00   2.7714e+02      3  SN      9.8236e-03   1.9597e+02   9.8800e-01
    5  00:00:00   2.7614e+02      4  BP      1.0001e-02   1.9526e+02   9.8800e-01
   10  00:00:00   2.6008e+02      5          1.0001e-02   1.8390e+02   9.8800e-01
   12  00:00:00   2.5424e+02      6  SN      1.0001e-02   1.7977e+02   9.8800e-01
   20  00:00:00   2.1008e+02      7          1.0001e-02   1.4854e+02   9.8800e-01
   30  00:00:00   1.6008e+02      8          1.0001e-02   1.1319e+02   9.8800e-01
   40  00:00:00   1.1008e+02      9          1.0001e-02   7.7834e+01   9.8800e-01
   50  00:00:01   6.0094e+01     10          1.0001e-02   4.2479e+01   9.8800e-01
   60  00:00:01   1.0191e+01     11          1.0001e-02   7.1235e+00   9.8800e-01
   62  00:00:01   1.9696e+00     12  SN      1.0001e-02   8.7073e-01   9.8800e-01
   63  00:00:01   1.5372e+00     13  SN      1.0001e-02  -8.8942e-06   9.8800e-01
   70  00:00:01   3.9955e+01     14          1.0001e-02  -2.8232e+01   9.8800e-01
   80  00:00:01   8.9939e+01     15          1.0001e-02  -6.3587e+01   9.8800e-01
   90  00:00:01   1.3993e+02     16          1.0001e-02  -9.8943e+01   9.8800e-01
  100  00:00:01   1.8993e+02     17  EP      1.0001e-02  -1.3430e+02   9.8800e-01

 STEP      TIME        ||U||  LABEL  TYPE           eps    po.period           om
    0  00:00:01   2.7877e+02     18  EP      1.0000e-02   1.9712e+02   9.8800e-01
   10  00:00:02   3.0266e+02     19  FP      1.1130e-02   2.1400e+02   9.8800e-01
   10  00:00:02   3.0266e+02     20  SN      1.1130e-02   2.1400e+02   9.8800e-01
   10  00:00:02   3.0359e+02     21          1.1129e-02   2.1467e+02   9.8800e-01
   20  00:00:02   3.5359e+02     22          9.0796e-03   2.5002e+02   9.8800e-01
   30  00:00:02   4.0359e+02     23          6.5243e-03   2.8538e+02   9.8800e-01
   34  00:00:03   4.2226e+02     24  FP      6.1417e-03   2.9858e+02   9.8800e-01
   34  00:00:03   4.2226e+02     25  SN      6.1417e-03   2.9858e+02   9.8800e-01
   36  00:00:03   4.3101e+02     26  PD      6.2859e-03   3.0476e+02   9.8800e-01
   40  00:00:03   4.5356e+02     27          8.0148e-03   3.2071e+02   9.8800e-01
   42  00:00:03   4.5892e+02     28  PD      8.1405e-03   3.2450e+02   9.8800e-01
   42  00:00:03   4.6194e+02     29  FP      8.1560e-03   3.2664e+02   9.8800e-01
   42  00:00:03   4.6195e+02     30  SN      8.1559e-03   3.2664e+02   9.8800e-01
   50  00:00:04   5.0355e+02     31          7.0447e-03   3.5606e+02   9.8800e-01
   60  00:00:04   5.5355e+02     32          5.3126e-03   3.9141e+02   9.8800e-01
   68  00:00:04   5.9322e+02     33  SN      4.5402e-03   4.1947e+02   9.8800e-01
   70  00:00:05   5.9929e+02     34  PD      4.5983e-03   4.2376e+02   9.8800e-01
   70  00:00:05   6.0103e+02     35          4.6567e-03   4.2499e+02   9.8800e-01
   80  00:00:05   6.0293e+02     36          4.8787e-03   4.2633e+02   9.8800e-01
   90  00:00:06   6.0292e+02     37          4.8946e-03   4.2633e+02   9.8800e-01
  100  00:00:06   6.0285e+02     38  EP      4.9361e-03   4.2628e+02   9.8800e-01
Constructing torus in reduced dynamical system

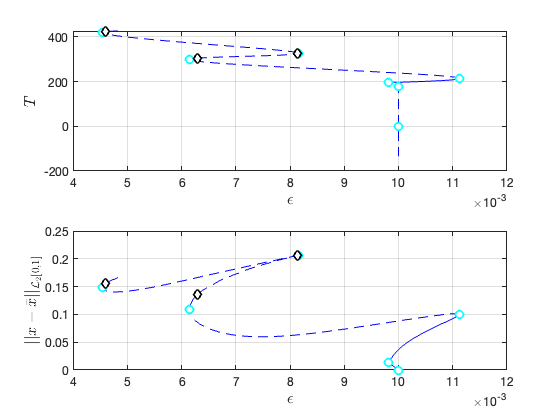
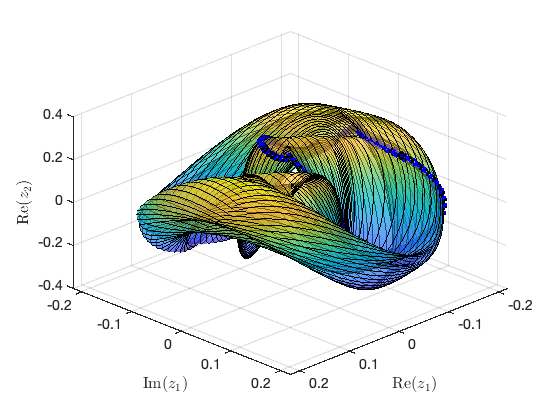
Illustration of the construction of torus in reduced dynamical system
Visualization of torus at (omega,epsilon)=(9.880000e-01,8.155992e-03)

 FRCs from ='po2.po': generating torus in physical domain.

SSM_HB2po:

under variation of $\epsilon$

set(S.contOptions, 'PtMX', 100, 'h_max', 0.5, 'bi_direct', false);
epsRange = [0.01 10]*epsilon;
S.SSM_HB2po('HBpo2_tr_cart','HB_tr_cart',2,'amp',epsRange,outdof,'saveICs');

 Run='HBpo2_tr_cart.po': Continue periodic orbits born from a HB point with label 2 of run HB_tr_cart.

    STEP   DAMPING               NORMS              COMPUTATION TIMES
  IT SIT     GAMMA     ||d||     ||f||     ||U||   F(x)  DF(x)  SOLVE
   0                          6.30e-06  1.14e+02    0.0    0.0    0.0
   1   1  1.00e+00  5.83e-05  1.35e-12  1.14e+02    0.0    0.0    0.0
   2   1  1.00e+00  5.04e-09  2.38e-15  1.14e+02    0.0    0.0    0.0

 STEP      TIME        ||U||  LABEL  TYPE           eps    po.period           om
    0  00:00:00   1.1400e+02      1  EP      5.0000e-02   8.0568e+01   9.6773e-01
   10  00:00:00   1.1416e+02      2          5.0191e-02   8.0690e+01   9.6773e-01
   20  00:00:00   1.1695e+02      3          5.2876e-02   8.2644e+01   9.6773e-01
   24  00:00:00   1.1849e+02      4  PD      5.4011e-02   8.3732e+01   9.6773e-01
   26  00:00:00   1.1968e+02      5  PD      5.4684e-02   8.4559e+01   9.6773e-01
   30  00:00:01   1.2193e+02      6          5.5519e-02   8.6153e+01   9.6773e-01
   35  00:00:01   1.2423e+02      7  SN      5.5787e-02   8.7776e+01   9.6773e-01
   35  00:00:01   1.2423e+02      8  FP      5.5787e-02   8.7776e+01   9.6773e-01
   40  00:00:01   1.2693e+02      9          5.5462e-02   8.9685e+01   9.6773e-01
   50  00:00:01   1.3192e+02     10          5.3523e-02   9.3219e+01   9.6773e-01
   60  00:00:01   1.3690e+02     11          5.0523e-02   9.6750e+01   9.6773e-01
   70  00:00:02   1.4188e+02     12          4.7012e-02   1.0028e+02   9.6773e-01
   80  00:00:02   1.4687e+02     13          4.3328e-02   1.0381e+02   9.6773e-01
   90  00:00:02   1.5185e+02     14          3.9686e-02   1.0733e+02   9.6773e-01
  100  00:00:02   1.5683e+02     15  EP      3.6248e-02   1.1086e+02   9.6773e-01
Constructing torus in reduced dynamical system

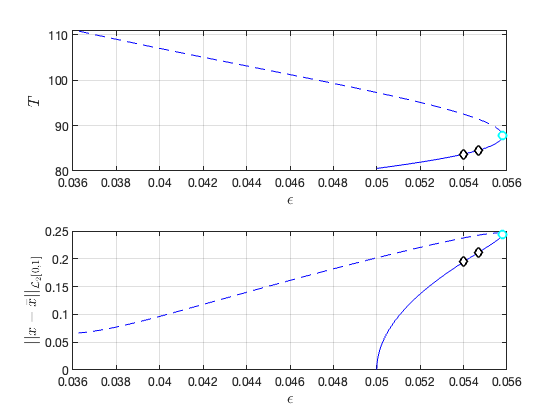
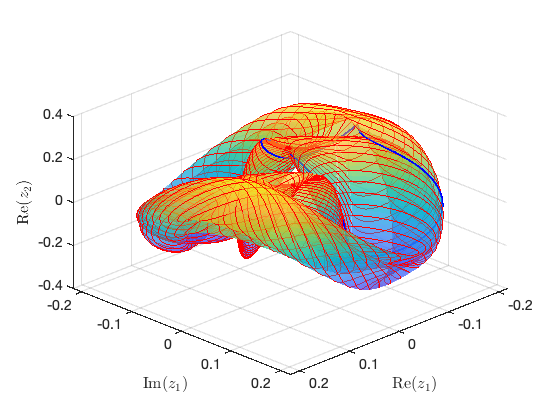
Illustration of the construction of torus in reduced dynamical system
Visualization of torus at (omega,epsilon)=(9.677295e-01,5.546229e-02)

 FRCs from ='HBpo2_tr_cart.po': generating torus in physical domain.

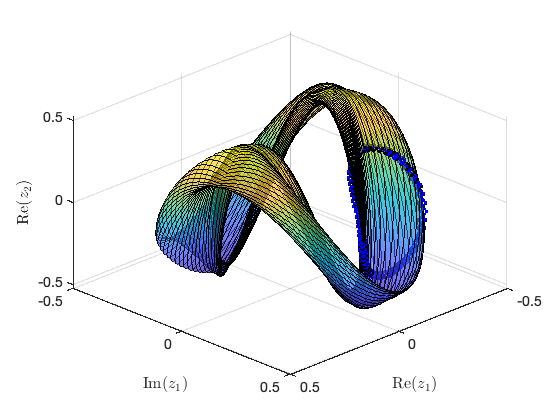
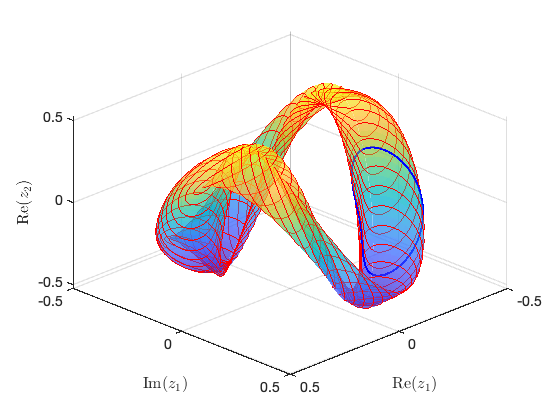
SSM_po2SN:

continuation of Saddle-Node bifurcation periodic orbits

SNLAB = 7;
set(S.contOptions, 'TOL', 1e-5);
epsRange = [2 8]*epsilon;
S.SSM_po2SN('SN','HBpo2_tr_cart',SNLAB,{freqRange,epsRange},outdof,'saveICs');

 Run='SN.po': Continue SN periodic orbits from label 7 of run HBpo2_tr_cart.

    STEP   DAMPING               NORMS              COMPUTATION TIMES
  IT SIT     GAMMA     ||d||     ||f||     ||U||   F(x)  DF(x)  SOLVE
   0                          2.19e-04  4.56e+02    0.0    0.0    0.0
   1   2  5.00e-01  2.88e-01  1.36e-04  4.56e+02    0.0    0.0    0.0
   2   1  1.00e+00  1.38e-01  8.06e-05  4.56e+02    0.0    0.0    0.0
   3   1  1.00e+00  3.02e-03  4.07e-07  4.56e+02    0.0    0.0    0.0
   4   1  1.00e+00  6.44e-06  3.97e-07  4.56e+02    0.0    0.0    0.0

 STEP      TIME        ||U||  LABEL  TYPE            om          eps    po.period
    0  00:00:00   4.5640e+02      1  EP      9.6773e-01   5.5794e-02   8.7769e+01
   10  00:00:00   4.6048e+02      2          9.6787e-01   5.5395e-02   8.8122e+01
   20  00:00:01   4.6538e+02      3          9.6805e-01   5.4922e-02   8.8545e+01
   30  00:00:01   4.7029e+02      4          9.6822e-01   5.4459e-02   8.8966e+01
   40  00:00:01   4.7520e+02      5          9.6839e-01   5.4004e-02   8.9383e+01
   50  00:00:02   4.8011e+02      6          9.6855e-01   5.3558e-02   8.9799e+01
   60  00:00:02   4.8502e+02      7          9.6871e-01   5.3120e-02   9.0211e+01
   70  00:00:03   4.8969e+02      8          9.6887e-01   5.2712e-02   9.0601e+01
   80  00:00:03   4.9403e+02      9          9.6901e-01   5.2339e-02   9.0961e+01
   90  00:00:04   4.9894e+02     10          9.6916e-01   5.1923e-02   9.1367e+01
  100  00:00:04   5.0386e+02     11  EP      9.6931e-01   5.1514e-02   9.1770e+01
Constructing torus in reduced dynamical system

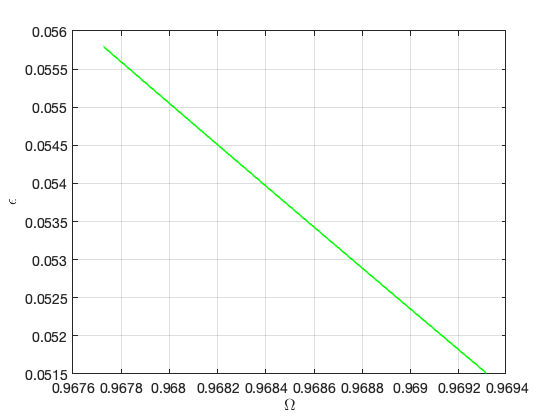
Illustration of the construction of torus in reduced dynamical system
Visualization of torus at (omega,epsilon)=(9.677269e-01,5.579409e-02)

FRCs from ='SN.po': generating torus in physical domain.

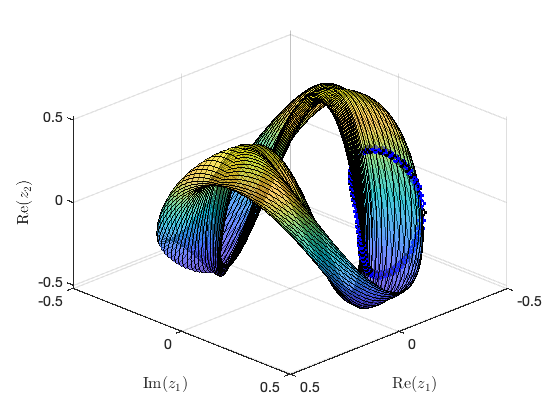
SSM_po2PD:

continuation of Period-doubling bifurcation periodic orbits

PDLAB = 4;
set(S.contOptions, 'h_min', 0.01, 'bi_direct', true, 'TOL', 1e-6);
S.SSM_po2PD('PD','HBpo2_tr_cart',PDLAB,{freqRange,epsRange},outdof,'saveICs');

 Run='PD.po': Continue PD periodic orbits from label 4 of run HBpo2_tr_cart.

    STEP   DAMPING               NORMS              COMPUTATION TIMES
  IT SIT     GAMMA     ||d||     ||f||     ||U||   F(x)  DF(x)  SOLVE
   0                          1.51e-07  1.20e+02    0.0    0.0    0.0

 STEP      TIME        ||U||  LABEL  TYPE            om          eps    po.period
    0  00:00:00   1.1982e+02      1  EP      9.6773e-01   5.4011e-02   8.3732e+01
   10  00:00:00   1.1661e+02      2          9.6674e-01   5.6565e-02   8.1437e+01
   20  00:00:01   1.1201e+02      3          9.6519e-01   6.0623e-02   7.8153e+01
   30  00:00:01   1.0738e+02      4          9.6349e-01   6.5211e-02   7.4863e+01
   40  00:00:02   1.0344e+02      5          9.6190e-01   6.9583e-02   7.2064e+01
   50  00:00:03   9.8531e+01      6          9.5971e-01   7.5722e-02   6.8579e+01
   57  00:00:03   9.5884e+01      7  EP      9.5822e-01   7.9999e-02   6.6406e+01

 STEP      TIME        ||U||  LABEL  TYPE            om          eps    po.period
    0  00:00:03   1.1982e+02      8  EP      9.6773e-01   5.4011e-02   8.3732e+01
   10  00:00:04   1.2059e+02      9          9.6796e-01   5.3433e-02   8.4282e+01
   20  00:00:05   1.2475e+02     10          9.6913e-01   5.0533e-02   8.7284e+01
   24  00:00:05   1.2525e+02     11  MX      9.6926e-01   5.0221e-02   8.7648e+01
Constructing torus in reduced dynamical system

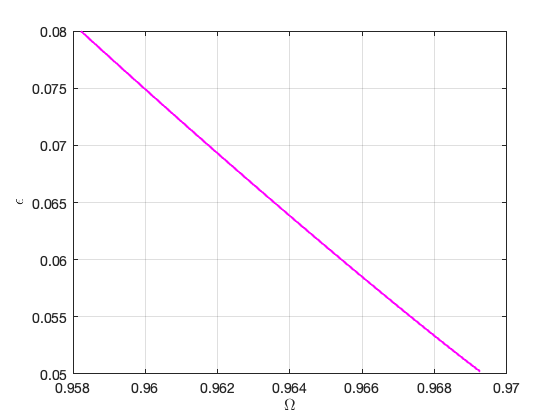
Illustration of the construction of torus in reduced dynamical system
Visualization of torus at (omega,epsilon)=(9.582154e-01,7.999920e-02)

 FRCs from ='PD.po': generating torus in physical domain.

Oscillatory System with a 2:1 internal resonance

Contents

Setup model

SSM computation

SSM_isol2ep:

FRCs on parametrisation space:

FRCs on physical space:

SSM_ep2HB:

Bifurcations occur for the following forcing parameters:

Bifurcations in parametrisation space:

Bifurcations in physical space:

SSM_ep2SN:

Bifurcations occur for the following forcing parameters:

Bifurcations in parametrisation space:

Bifurcations in physical space:

SSM_HB2po:

Plot quasiperiodic FRC

SSM_po2po:

SSM_HB2po:

SSM_po2SN:

SSM_po2PD: